Funcions
Funcions
- 2009 - Juny - sèrie 4 - 3.  - 2009 - Juny - sèrie 4 - 6.  - 2009 - Juny - sèrie 3 - 1.  - 2009 - Juny - sèrie 3 - 3.  - 2009 - Setembre - sèrie 1 - 3.  - 2009 - Setembre - sèrie 1 - 6.  - 2010 - Juny - sèrie 1 - 1.  - 2010 - Juny - sèrie 1 - 2.  - 2010 - Juny - sèrie 1 - 4.  - 2010 - Juny - sèrie 4 - 2.  - 2010 - Juny - sèrie 4 - 3.  - 2010 - Juny - sèrie 4 - 6.  - 2010 - Juny - sèrie 5 - 2.  - 2010 - Juny - sèrie 5 - 4.  - 2010 - Juny - sèrie 5 - 5.  - 2010 - Setembre - sèrie 2 - 2.  - 2010 - Setembre - sèrie 2 - 3.  - 2010 - Setembre - sèrie 2 - 6.  - 2011 - Juny - sèrie 1 - 3.  - 2011 - Juny - sèrie 1 - 5.  - 2011 - Juny - sèrie 1 - 6.  - 2011 - Juny - sèrie 4 - 1.  - 2011 - Juny - sèrie 4 - 4.  - 2011 - Juny - sèrie 4 - 6.  - 2011 - Setembre - sèrie 2 - 1.  - 2011 - Setembre - sèrie 2 - 4.  - 2011 - Setembre - sèrie 2 - 6.  - 2012 - Juny - sèrie 3 - 1.  - 2012 - Juny - sèrie 3 - 5.  - 2012 - Setembre - sèrie 4 - 1.  - 2012 - Setembre - sèrie 4 - 2.  - 2012 - Setembre - sèrie 4 - 5.  - 2013 - Juny - sèrie 4 - 1.  - 2013 - Juny - sèrie 4 - 3.  - 2013 - Juny - sèrie 4 - 4.  - 2013 - Juny - sèrie 4 - 6.  - 2013 - Setembre - sèrie 1 - 1. 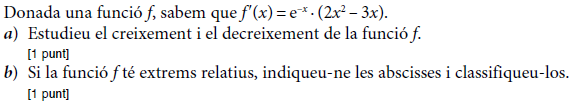 - 2013 - Setembre - sèrie 1 - 6.  - 2014 - Setembre - sèrie 5 - 2.  - 2014 - Setembre - sèrie 5 - 3.  - 2014 - Setembre - sèrie 5 - 6.  - 2015 - Juny - sèrie 2 - 1.  - 2015 - Juny - sèrie 2 - 3.  - 2015 - Juny - sèrie 2 - 5.  - 2015 - Juny - sèrie 4 - 2.  - 2015 - Juny - sèrie 4 - 3.  - 2015 - Juny - sèrie 4 - 5. 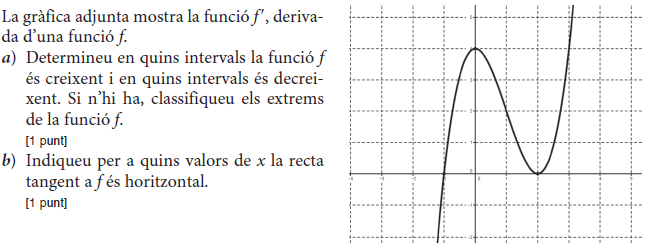 - 2015 - Setembre - sèrie 5 - 2.  - 2015 - Setembre - sèrie 5 - 3.  - 2015 - Setembre - sèrie 5 - 4.  - 2016 - Juny - sèrie 3 - 1.  - 2016 - Juny - sèrie 3 - 2.  - 2016 - Juny - sèrie 3 - 4.  - 2016 - Setembre - sèrie 1 - 2.  - 2016 - Setembre - sèrie 1 - 3.  - 2016 - Setembre - sèrie 1 - 5.  - 2017 - Juny - sèrie 1 - 1.  - 2017 - Juny - sèrie 1 - 2.  - 2017 - Juny - sèrie 1 - 6.  - 2017 - Juny - sèrie 5 - 4.  - 2017 - Juny - sèrie 5 - 5.  - 2017 - Setembre - sèrie 2 - 2.  - 2017 - Setembre - sèrie 2 - 3.  - 2017 - Setembre - sèrie 2 - 6. 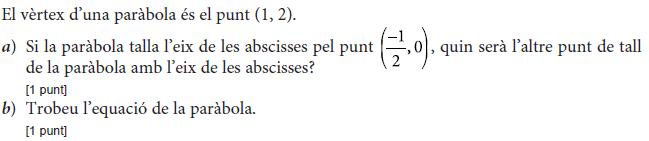 - 2019 - Juny - sèrie 1 - 3. La gràfica de la funció `f(x)=ax+b+8/x` passa pel punt `(–2, –6)` i la recta tangent en aquest punt és paraŀlela a l’eix de les abscisses.
[1 punt] b) Calculeu el valor de b. [1 punt] - 2019 - Juny - sèrie 1 - 4. La funció `f(x)=40/(x^2-22x+125)` mostra aproximadament la venda diària, en milers d'unitats, d'un perfum de moda en funció de `x`, en que `x` és el dia del mes de febrer
[0,75 punts] b) Quin dia del mes de febrer es van vendre més perfums i quantes unitats se’n van vendre? [1,25 punts] - 2019 - Juny - sèrie 4 - 1. Considereu la funció `f(x)=2x^3+ax`. Calculeu el valor de la constant `a` per tal que aquesta funció tingui un extrem relatiu en el punt d’abscissa `x = –1`. Digueu si es tracta d’un màxim o d’un mínim i doneu també el valor que pren la funció `f(x)` en aquest punt. [2 punts] - 2019 - Juny - sèrie 4 - 3. Un nutricionista, després de fer un estudi personalitzat a un pacient, li proposa una dieta. Segons el model del nutricionista, el pes en kilograms del pacient seguirà la funció `f(x)=(63x+510)/(x+6)`, en què `x` denota el nombre de mesos que fa que segueix la dieta.
[0,75 punts] b) Determineu el pes inicial del pacient i quant pesarà al cap de dos mesos de seguir la dieta segons el model. Cap a quin valor tendirà el seu pes a llarg termini? Argumenteu si aquest valor límit s’assolirà en algun moment. [1,25 punts] - 2019 - Juny - sèrie 4 - 5. Un comerciant pot comprar articles a `350 €` la unitat. Si els ven a `750 €` la unitat, en ven `30`. Sabem que la relació entre aquestes dues variables (el preu de venda i el nombre d’unitats venudes) és lineal i que, per cada descompte de `20` € en el preu de venda, incrementa les vendes en `3` unitats. Considerant que el comerciant només comprarà el nombre d’articles que sap que vendrà:
[1 punt] b) Determineu el preu de venda que fa màxims els beneficis del comerciant i justifiqueu que és un màxim. Determineu quantes unitats vendrà. [1 punt] - 2019 - Setembre - sèrie 5 - 2. Per a la campanya d’aquest estiu, una botiga d’esports que ven patinets elèctrics espera vendre `40` patinets a un preu de `1.000 €` per patinet. Segons un estudi de mercat, la relació entre el nombre de vegades que es rebaixa el preu del patinet en `50 €` i el nombre de patinets venuts és lineal, i, per cada `50 €` de rebaixa en el preu de venda de cada patinet, hi haurà un increment de les vendes de `10` patinets més.
b) Trobeu quin ha de ser el preu del patinet per tal d’obtenir els ingressos màxims. Trobeu també el nombre de patinets que es vendran i els ingressos que s’obtindran amb aquest preu. [1 punt] - 2019 - Setembre - sèrie 5 - 3. Es preveu un canvi important en la població d’una determinada zona per qüestions mediambientals. El nombre d’habitants de la zona, en milions, vindrà donat per la funció `P(t)=(t^2+28)/(t+2)^2`, en què `t` mesura el temps en anys des del moment actual `(t = 0)`.
b) En quin moment s’arribarà al nombre mínim d’habitants? Quants habitants hi haurà en aquell moment? Quin és el nombre màxim d’habitants que s’assoleix en aquesta zona? [1 punt] - 2019 - Setembre - sèrie 5 - 5. Considereu una funció `f(x)` que té com a primera derivada `f'(x) = 2x^2 + bx + 4`, en què `b` és un paràmetre real.
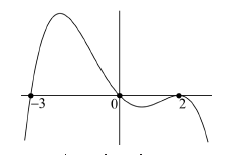
b) Si sabem que la gràfica de la funció `f(x)` passa pel punt `(0, 3)`, trobeu l’equació de la recta tangent a `f(x)` en aquest punt. [1 punt] - Sigui `f (x) = 2x^3 – x^2 + 3x + 1`. Donades les rectes `r_1: y = x + 2` i `r_2: y = 7x – 2`: a) Expliqueu, raonadament, si alguna de les dues rectes pot ser tangent a la corba `y = f (x)` en algun punt. b) En cas que alguna d’elles ho sigui, trobeu el punt de tangència. [1 punt per cada apartat] - Considereu la funció real de variable real, `f(x)=(2x^3)/(x^2-1)`. a) Trobeu-ne el domini. b) Calculeu l’equació de les seves asímptotes, si en té. c) Estudieu-ne els intervals de creixement i de decreixement, així com les abscisses els seus extrems relatius, si en té, i classifiqueu-los. [0,5 punts per l’apartat a; 1,5 punts per l’apartat b; 2 punts per l’apartat c] - Sigui `P(x) = ax^2+ bx + c` un polinomi qualsevol de segon grau. a) Trobeu la relació existent entre els paràmetres `a`, `b` i `c` sabent que es compleix que `P(1) = 0` i `P(2) = 0`. b) Quan es compleix la condició anterior, indiqueu quins valors pot tenir `P'(3/2)`. [1 punt per cada apartat] - Sigui `f (x)=x^2 · e^(–ax)` quan `a≠0`. a) Calculeu el valor de a perquè aquesta funció tingui un extrem relatiu en el punt d’abscissa `x=2`. b) Quan `a=2`, classifiqueu-ne els extrems relatius. [1 punt per cada apartat] - La gràfica corresponent a la derivada d'una funció f(x) és la següent: a) Expliqueu raonadament quins valors de `x` corresponen a màxims o a mínims de relatius de `f(x)`. b) Determineu els intervals de creixement i decreixement de la funció `f(x)`. [1,5 punts per l'apartat a; 0,5 punts per l'apartat b] |

Bună, vreau doar să le spun tuturor că am primit împrumutul meu de 1.000.000,00 USD de la programul de investiții pentru împrumutul domnului Ben și sunt 100% contact legitim prin e-mail: 247officedept@gmail.com sau Trimiteți-i text pe WhatsApp + 1-989-394-3740 . dacă căutați finanțare de 100% la o rată scăzută de 2% în schimb.
ResponElimina